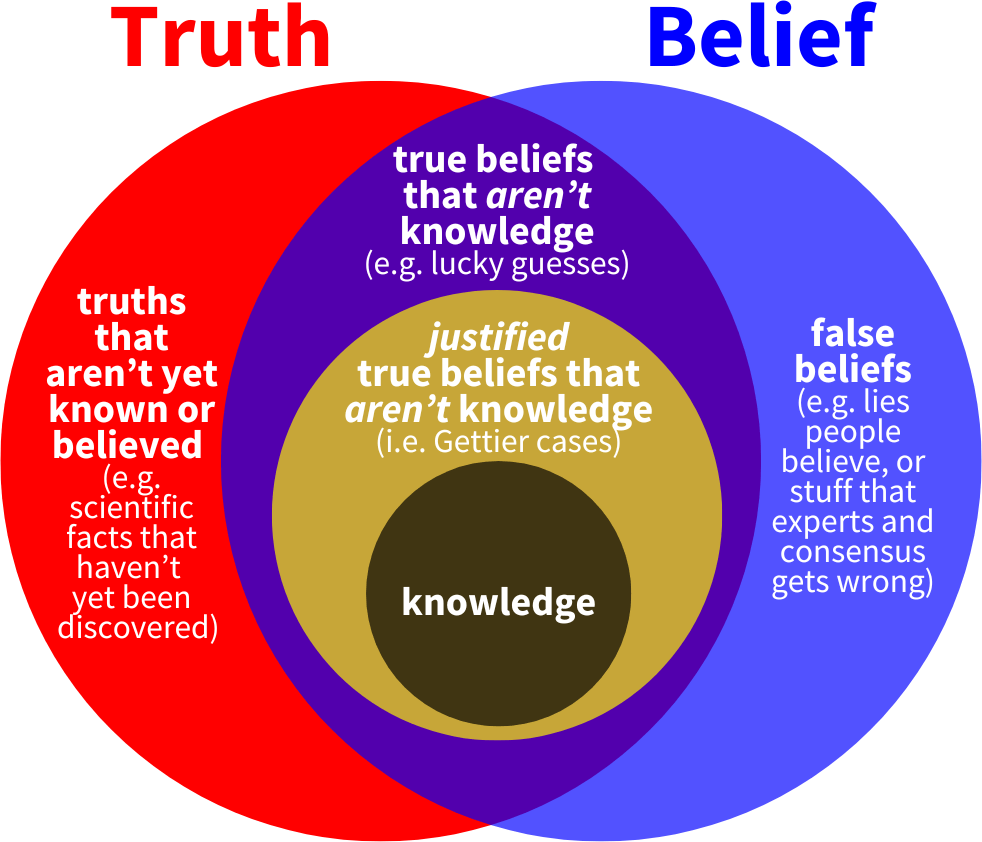
Overview – The Definition of Knowledge
The definition of knowledge is one of the oldest questions of philosophy. Plato’s answer, that knowledge is justified true belief, stood for thousands of years – until a 1963 philosophy paper by philosopher Edmund Gettier challenged this definition.
Gettier described two scenarios – now known as Gettier cases – where an individual has a justified true belief but that is not knowledge.
Since Gettier’s challenge to the justified true belief definition, various alternative accounts of knowledge have been proposed. The goal of these accounts is to define ‘knowledge’ in a way that rules out Gettier cases whilst still capturing all instances of what we consider to be knowledge.
A Level philosophy looks at 5 definitions of knowledge:
- Justified true belief (the tripartite definition)
- JTB + No false lemmas
- Reliabilism
- Virtue epistemology
- Infallibilism
It’s important to first distinguish the kind of knowledge we’re discussing here. Broadly, there are three kinds of knowledge:
- Ability: knowledge how – e.g. “I know how to ride a bike”
- Acquaintance: knowledge of – e.g. “I know Fred well”
- Propositional: knowledge that – e.g. “I know that London is the capital of England”
When we talk about the definition of knowledge, we are talking about the definition of propositional knowledge specifically.
Justified True Belief
The tripartite definition
In Theaetetus, Plato argues that knowledge is “true belief accompanied by a rational account”. This got simplified to:
- Justified
- True
- Belief
‘Justified true belief’ is known as the tripartite definition of knowledge.
Necessary and sufficient conditions
The name of the game in defining ‘knowledge’ is to provide necessary and sufficient conditions.
For example, ‘unmarried’ and ‘man’ are both necessary to be a ‘bachelor’ because if you don’t meet both these conditions you’re not a bachelor. Further, being an ‘unmarried man’ is sufficient to be a ‘bachelor’ because everything that meets these conditions is a bachelor. So, ‘unmarried man’ is a good definition of ‘bachelor’ because it provides both the necessary and sufficient conditions of that term.
The correct definition of ‘knowledge’ will work the same way. Firstly, we can argue that ‘justified’, ‘true’, and ‘belief’ are all necessary for knowledge.
For example, you can’t know something if it isn’t true. If someone said, “I know that the moon is made of green cheese” you wouldn’t consider that knowledge because it isn’t true.
Similarly, you can’t know something you don’t believe. It just wouldn’t make sense, for example, to say “I know today is Monday but I don’t believe today is Monday.”
And finally, justification. Suppose someone asks you if you know how many moons Pluto has. You have no interest in astronomy but just have a strong feeling about the number 5 because it’s your lucky number or whatever. You’d be right – Pluto does indeed have 5 moons – but it seems a bit of a stretch to say you knew Pluto has 5 moons. Your true belief “Pluto has 5 moons” is not properly justified and so would not count as knowledge.
So, ‘justified’, ‘true’, and ‘belief’ may each be necessary for knowledge. But are these conditions sufficient? If ‘justified true belief’ is also a sufficient definition of knowledge, then everything that is a justified true belief will be knowledge. However, this is challenged by Gettier cases.
Problem: Gettier cases
Gettier’s paper describes two scenarios where an individual has a justified true belief that is not knowledge. Both scenarios describe a belief that fails to count as knowledge because the justified belief is only true as a result of luck.
Gettier case 1
- Smith and Jones are interviewing for the same job
- Smith hears the interviewer say “I’m going to give Jones the job”
- Smith also sees Jones count 10 coins from his pocket
- Smith thus forms the belief that “the man who will get the job has 10 coins in his pocket”
- But Smith gets the job, not Jones
- Then Smith looks in his pocket and, by coincidence, he also has 10 coins in his pocket
Smith’s belief “the man who will get the job has 10 coins in his pocket” is:
- Justified: he hears the interviewer say Jones will get the job and he sees that Jones has 10 coins in his pocket
- True: the man who gets the job (Smith) does indeed have 10 coins in his pocket
But despite being a justified true belief, we do not want to say that Smith’s belief counts as knowledge because it’s just luck that led to him being correct.
This shows that the tripartite definition of knowledge is not sufficient: you can have a justified true belief that is not knowledge.
@philosophymania Gettier cases aim to show justified true belief is not sufficient for knowledge https://philosophyalevel.com/aqa-philosophy-revision-notes/definition-of-knowledge/ #philosophy #philosophytiktok #epistemology #alevelphilosophy ♬ original sound – philosophymania
Gettier case 2
Gettier’s second example relies on the logical principle of disjunction introduction (or, more simply, addition).
Disjunction introduction says that if you have a true statement and add “or some other statement” then the full statement (i.e. “true statement or some other statement”) is also true.
For example: “London is the capital of England” is true. And so the statement “either London is the capital of England or the moon is made of green cheese” is also true, because London is the capital of England. Even though the second part (“the moon is made of green cheese”) is false, the overall statement is true because the or means only one part has to be true (in this case “London is the capital of England”).
Gettier’s second example is as follows:
- Smith has a justified belief that “Jones owns a Ford”
- So, using the principle of disjunctive introduction above, Smith can form the further justified belief that “Either Jones owns a Ford or Brown is in Barcelona”
- Smith thinks his belief that “Either Jones owns a Ford or Brown is in Barcelona” is true because the first condition is true (i.e. that Jones owns a Ford)
- But it turns out that Jones does not own a Ford
- However, by sheer coincidence, Brown is in Barcelona
So, Smith’s belief that “Either Jones owns a Ford or Brown is in Barcelona” is:
- True: “Either Jones owns a Ford or Brown is in Barcelona” turns out to be true. But Smith thought it was true because of the first condition (Jones owns a Ford) whereas it turns out it is true because of the second condition (Brown is in Barcelona)
- Justified: The original belief “Jones owns a Ford” is justified, and so disjunction introduction means that the second belief “Either Jones owns a Ford or Brown is in Barcelona” is also justified.
But despite being a justified true belief, it is wrong to say that Smith’s belief counts as knowledge, because it was just luck that led to him being correct.
This again shows that the tripartite definition of knowledge is not sufficient.
Problem: Not necessary
The majority of this debate focuses on whether the tripartite definition is sufficient for knowledge, but you can potentially argue that one or more of the conditions are not necessary:
- Justification: The fact that children and animals appear to possess knowledge suggests that justification is not necessary for knowledge because children and animals have knowledge even though they can’t justify it.
- Truth: Zagzebski’s definition of knowledge does not explicitly include true as a condition but instead talks about acts of intellectual virtue (which kind of implies truth but anyway). Some philosophers reject the very idea of objective truth, but that’s getting a bit off-piste.
- Belief: You can potentially imagine scenarios where someone knows something but doesn’t believe it. For example, you may have heard years ago that Pluto has 5 moons but forgotten it consciously. But when asked years later “how many moons does Pluto have?” you correctly answer “5” – even though you’re not sure about this answer and don’t really believe it.
Alternative definitions of knowledge
Gettier cases are a devastating problem for the tripartite definition of knowledge.
In response, philosophers have tried to come up with new definitions of knowledge that avoid Gettier cases.
Generally, these new definitions seek to refine the justification condition of the tripartite definition. True and belief remain unchanged.
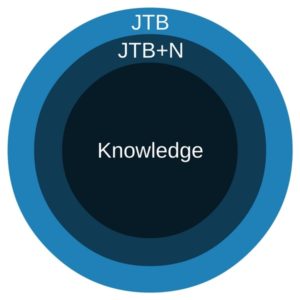
JTB + no false lemmas
The no false lemmas definition of knowledge aims to strengthen the justification condition of the tripartite definition.
It says that James has knowledge of P if:
- P is true
- James believes that P
- James’s belief is justified
- James did not infer that P from anything false
So, basically, it adds an extra condition to the tripartite definition. It says knowledge is justified true belief + that is not inferred from anything false (a false lemma).
This avoids the problems of Gettier cases because Smith’s belief “the man who will get the job has 10 coins in his pocket” is inferred from the false lemma “Jones will get the job”.
Remember:
- The tripartite definition says Smith’s belief is knowledge, even though it isn’t
- The no false lemmas response says Smith’s belief is not knowledge, which is correct.
So, in this instance, the no false lemmas definition appears to be a more accurate account of knowledge than the tripartite view: it avoids saying Gettier cases count as knowledge.
Problem: fake barn county
However, the no false lemmas definition of knowledge faces a similar problem: the fake barn county situation:
- In ‘fake barn county’, the locals create fake barns that look identical to real barns
- Henry is driving through fake barn county, but he doesn’t know the locals do this
- Henry often thinks “there’s a barn” when he looks at the fake barns
- These beliefs are not knowledge, because they are not true – the barns are fake
- However, on one occasion Henry looks at the one real barn and thinks “there’s a barn”
- This time the belief is true
- It’s also justified by his visual perception of the barn
- And it’s not inferred from anything false.
According to the no false lemmas definition, Henry’s belief is knowledge.
But this shows that the no false lemmas definition must be false. Henry’s belief is clearly not knowledge – he’s just lucky in this instance.
Reliabilism
Reliabilism says James knows that P if:
- P is true
- James believes that P
- James’s belief that P is caused by a reliable method
A reliable method is one that produces a high percentage of true beliefs.
So, if you have good eyesight, it’s likely that your eyesight would constitute a reliable method of forming true beliefs. If you have an accurate memory, it’s likely your memory would also be a reliable method for forming true beliefs. If a website is consistent in reporting the truth, that website would also count as a reliable method.
But if you form a belief through an unreliable method – for example by simply guessing or using a biased source – then it would not count as knowledge even if the resultant belief is true.
Children and Animals
An advantage of reliabilism is that it allows for young children and animals to have knowledge. Typically, we attribute knowledge to young children and animals. For example, it seems perfectly sensible to say that a seagull knows where to find food or that a baby knows when its mother is speaking.
However, pretty much all the other definitions of knowledge considered here imply that animals and young children can not have knowledge. For example, a seagull or a baby can’t justify its beliefs and so justified true belief rules out seagulls and young babies from having knowledge. Similarly, if virtue epistemology is the correct definition, it is hard to see how a seagull or a newly born baby could possess intellectual virtues of care about forming true beliefs and thus possess knowledge.
However, both young children and animals are capable of forming beliefs via reliable processes, e.g. their eyesight, and so according to reliabilism are capable of possessing knowledge.
Problem: fake barn county
You can argue against reliabilism using the same fake barn county argument above: Henry’s true belief that “there’s a barn” is caused by a reliable process – his visual perception. Reliabilism would thus (incorrectly) say that Henry knows “there’s a barn” even though his belief is only true as a result of luck.
Virtue epistemology
There are several forms of virtue epistemology (we will look at two), but common to all virtue epistemology definitions of knowledge is a link between a belief and intellectual virtues. Intellectual virtues are somewhat analogous to the sort of moral virtues considered in Aristotle’s virtue theory in moral philosophy. However, instead of being concerned with moral good, intellectual virtues are about epistemic good. For example, an intellectually virtuous person would have traits such as being rational, caring about what’s true, and a good memory.
Linda Zagzebski: What is Knowledge?
Formula for creating Gettier-style cases
Philosopher Linda Zagzebski argues that definitions of knowledge of the kind we have looked at so far (i.e. ‘true belief + some third condition’) will always fall victim to Gettier-style cases. She provides a formula for constructing such Gettier cases to defeat these definitions:
- Start with a situation where there is a belief that fits the definition (‘true belief + some third condition’) but is false due to bad luck
- E.g. Henry’s belief “there’s a barn” when he is looking at the fake barns
- Then change the situation to one where the belief fits that definition (‘true belief + some third condition’) but is true due to good luck
- E.g. Henry’s belief “there’s a barn” when he is looking at the one real barn
- In the second case, the belief will still fit the definition (‘true belief + some third condition’) because it’s basically the same as the first case
- But the second case won’t be knowledge, because it’s only true due to luck
Zagzebski argues that this formula will always provide a means to defeat any definition of knowledge that takes the form ‘true belief + some third condition’ (whether that third condition is justification, formed by a reliable process, or whatever).
The reason for this is that truth and the third condition are simply added together, but not linked (the belief is not apt, to use Sosa’s terminology). The fact that truth and the third condition are not linked leaves a gap where lucky cases can incorrectly fit the definition.
Zagzebski’s definition of knowledge
The issues resulting from the gap between truth and the third condition motivate Zagzebski to do away with the ‘truth’ condition altogether. Instead, Zagzebski’s analysis of knowledge is that James knows that P if:
- James believes that P
- James’s belief that P arises from an act of intellectual virtue
However, in Zagzebski’s analysis of knowledge, the ‘truth’ of the belief is kind of implied by the idea of an act of intellectual virtues. This can be shown by drawing a comparison with moral virtue:
An act of moral virtue is one where the actor both intends to do good and achieves that goal. For example, intending to help an old lady across the road but killing her in the process is not an act of moral virtue because it doesn’t achieve a virtuous goal (despite the virtuous intent). Likewise, helping the old lady across the road because you think she will give you money is not an act of moral virtue – even though it succeeds in achieving a virtuous goal – because your intentions aren’t good.
Intellectual virtue is similar: You must both have the correct motivation (e.g. you want to find the truth) and succeed as a result of that virtue (i.e. your belief turns out to be true because you acted virtuously).
Virtues motivate us to pursue what is good. In the case of knowledge, good knowledge is also true. Secondly, virtues enable us to achieve our goals (in the same way a virtuous i.e. good knife enables you to cut) and so intellectual virtues would enable you to reliably form true beliefs.
Sosa’s virtue epistemology
Another virtue epistemology approach to knowledge is Ernest Sosa’s definition of apt belief.
Sosa uses the following analogy to argue that knowledge, like a virtuous shot in archery, has the following three properties: Accuracy, adroitness, and aptness.
| Archery | Knowledge | |
| Accuracy | The arrow hits the target. | The belief is true. |
| Adroitness | The archer is skilled. | The believer is intellectually virtuous. |
| Aptness | The arrow hits the target because of the archer’s skill, not just luck. | The belief is true because of the believer’s intellectual virtues. |
This last condition – aptness – differentiates Sosa’s understanding of knowledge from those criticised by Zagzebski above. According to Sosa, for something to qualify as knowledge the belief must be true as a direct consequence of the believer exercising their intellectual virtues – it must be apt. Aptness provides a link between truth and the third condition that rules out Gettier-style situations where the belief is only true as a result of luck.
Returning to the fake barn county example, Sosa’s virtue epistemology could (correctly) say Henry’s belief “there’s a barn” in fake barn county would not qualify as knowledge – despite being true and formed by a reliable method – because it is not apt. Yes, Henry’s belief is accurate (i.e. true) and adroit (i.e. Henry has good eyesight etc.), but he only formed the true belief as a result of luck, not because he used his intellectual virtues.
Problem: children and animals
As mentioned in more detail in the reliabilism section above, a potential criticism of virtue epistemology is that it appears to rule out the possibility of young children or babies possessing knowledge, despite the fact that they arguably can know many things.
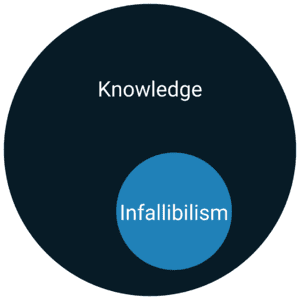
Infallibilism
Infallibilism argues that for a belief to count as knowledge, it must be true and justified in such a way as to make it certain.
So, even though Smith has good reasons for his beliefs in the Gettier case, they’re not good enough to provide certainty. Certainty, to philosophers like Descartes, means the impossibility of doubt.
In the Gettier case, Smith might have misheard the interviewer say he was going to give Jones the job. Or, even more extreme, Smith might be a brain in a vat and Jones may not even exist! Either of these scenarios – however unlikely – raise the possibility of doubt.
Problem: too strict
So, infallibilism correctly says Smith’s belief in the Gettier case does not count as knowledge.
But it also says pretty much everything fails to qualify as knowledge!
“I know that water boils at 100°c” – can this be doubted? Of course it can! Your science teachers might have been lying to you, you might have misread your thermometer, you might be a brain in a vat and there’s no such thing as water!
Pretty much any belief can be doubted, as Descartes demonstrates in his three waves of doubt.
So, whereas Gettier cases show the tripartite definition to set the bar too low for knowledge, infallibilism sets the bar way too high – barely anything can be known! In other words, we can argue that certainty is not a necessary condition of knowledge.