Dating back at least as far as Aristotle in the 4th Century BC, the Square of Opposition is a visual framework for representing the logical connections and relationships between four basic categorical propositions:
- A: All S are P
- E: No S is P
- I: Some S are P
- O: Some S are not P
These propositions express information about the classes or categories of objects or individuals. The square of opposition below represents how these propositions relate to each other:
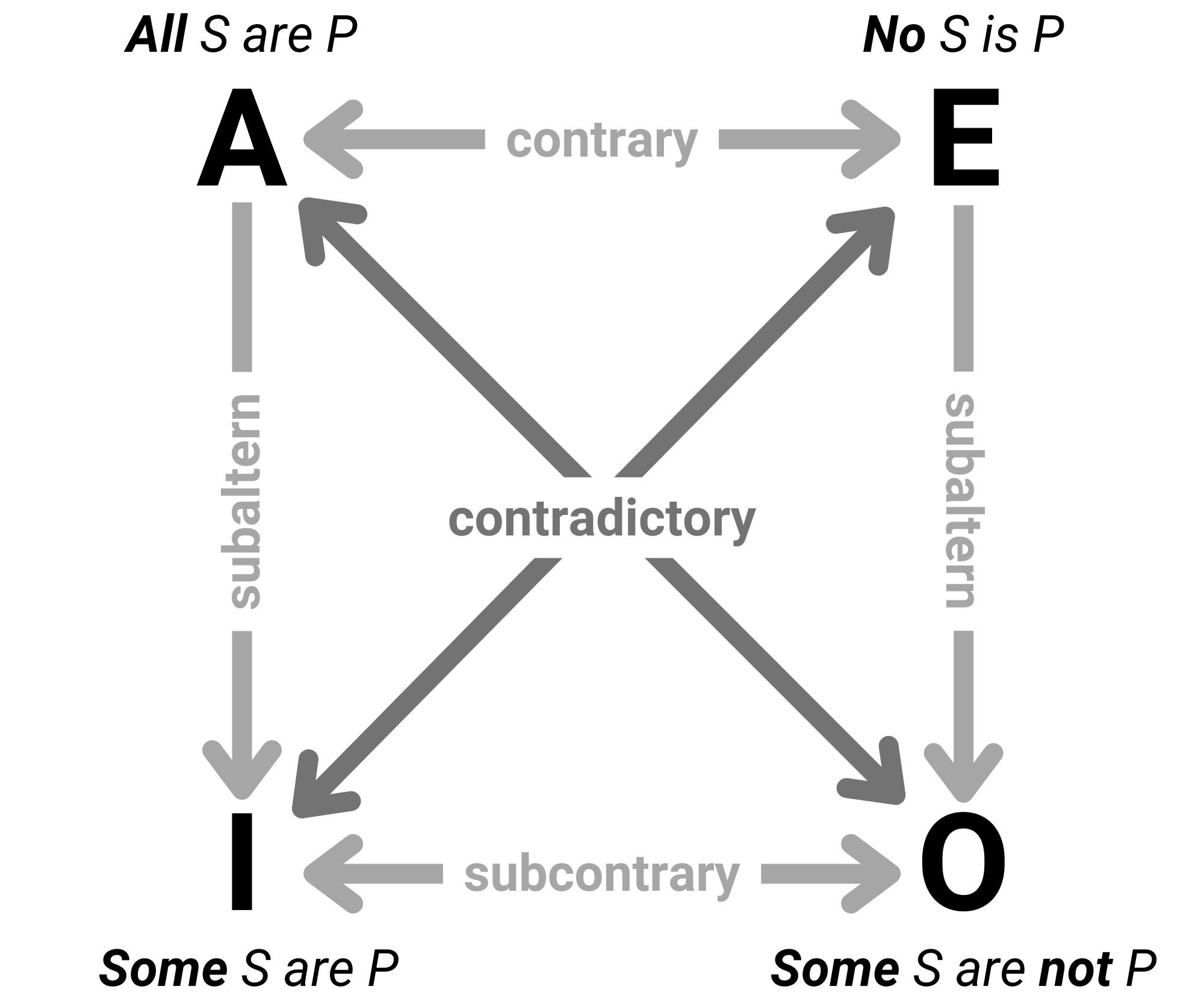
Note: This is the traditional square of opposition. These relationships don’t necessarily hold in the modern square of opposition.
1. Contradictory Pairs:
A proposition (All S are P) and O proposition (Some S are not P) are contradictories, as are E proposition and I proposition.
When propositions are contradictory, the truth of one proposition implies the falsity of the other and vice versa. In other words, if one is true the other must be false, and if one is false the other must be true.
For example:
- A: All cats are mammals
- O: Some cats are not mammals
If all cats are mammals (A proposition) is true, then it must be false that some cats are not mammals (O proposition). If one proposition is true, the other must be false.
And vice versa: If all cats are mammals (A proposition) were false, then it would be true that some cats are not mammals (O proposition).
Another example:
- E: No mammals can fly
- I: Some mammals can fly
Again, these propositions directly contradict each other: If no mammals can fly (E proposition), then it must be false that some mammals can fly (I proposition) and vice versa.
2. Contrary Pairs:
A proposition (All S are P) and E proposition (No S are P) are contraries.
When propositions are contrary, they cannot both be true simultaneously. In other words, if one is true, the other must be false.
However, although it’s impossible for contraries to both be true, it is possible for both contraries to be false.
For example:
- A: All birds can fly
- E: No birds can fly
In this example, both statements are false. A claims that all birds can fly, but we know there are flightless birds like penguins and ostriches, which makes this statement false. On the other hand, E asserts that no birds can fly, which is also false.
However, if A proposition were true (all birds could fly), then it would be impossible for E proposition to also be true (no birds can fly).
3. Subcontrary Pairs:
I proposition (Some S are P) and O proposition (Some S are not P) are subcontraries.
When propositions are subcontrary, they cannot both be false simultaneously. In other words, if one is false, the other must be true.
However, although it’s impossible for contraries to both be true, it is possible for both contraries to be true.
For example:
- I: Some cats are friendly
- E: Some cats are not friendly
In this example, both statements are true. I claims that some cats are friendly, and some cats are indeed friendly. E claims that some cats are not friendly, and this is also true.
4. Subalternation Pairs:
A proposition (All S are P) implies the corresponding I proposition (Some S are P). Similarly, E proposition (No S are P) implies the corresponding O proposition (Some S are not P). These pairs are known as subalterns.
When propositions are subalterns, the truth of the universal proposition implies the truth of the specific proposition.
However, notice that the arrow on the diagram only goes one way: The truth of the specific proposition (I or O) does not imply the corresponding universal proposition (A or E).
For example:
- A: All mammals have hair
- I: Some mammals have hair
In this example, if we accept the A proposition that all mammals have hair, the I proposition that some mammals have hair logically follows. So, the truth of the universal A proposition implies the corresponding particular I proposition.
However, all mammals have hair (A proposition) does not logically follow from some mammals have hair (I proposition).
Another example:
- E: No birds can swim
- O: Some birds can not swim
Again, the truth of the universal E proposition implies the truth of the specific O proposition: If it’s true that no birds can swim, then it’s true that some birds can’t swim.
And again, it doesn’t work the other way though: Just because some birds can’t swim (O proposition), it doesn’t necessarily mean no birds can swim (E proposition).
The modern vs. traditional square of opposition
The difference between the traditional and modern squares of opposition lies in the treatment of existential import. The traditional square assumes the existence of the subject class in universal statements, while the modern square does not.
The traditional square: Universal import
So, in the traditional square of opposition, when we say “All S are P,” it is implied that there are actually some S that exist. If no S exist, then the statement “All S are P” would be considered false.
For example:
- A: All unicorns are white
- This statement would be false, because unicorns don’t exist
- E: No unicorns are white
- This statement would also be false, because unicorns don’t exist
The problem with the traditional square of opposition is that the relationships it describes don’t hold when the S is empty.
For example, the traditional square says that if A is true, then O must be false because they are contradictories. But this doesn’t work with unicorns: All unicorns are white (A) is false, and some unicorns are not white (O) is also false.
The modern square: No universal import
However, the modern square of opposition removes the assumption of universal import. Instead, it adopts a more abstract approach where universal statements do not imply the existence of members of the subject class. This means that “All S are P” can be true even if there are no S that exist, because it’s considered a vacuously true statement.
For example:
- A: All unicorns are white
- This statement is treated as true – even though unicorns don’t exist – because there are no unicorns that disprove this claim
- E: No unicorns are white
- This statement would also be treated as true – even though unicorns don’t exist – because, again, there are no unicorns that disprove this claim
However, although universal statements (A and E) do not have existential import in the modern square, particular statements (I and O) do.
A consequence of this is that the I proposition no longer follows from the A proposition according to the modern square of opposition.
For example:
- A: All unicorns are white
- This statement would be considered vacuously true, but it does not follow that:
- I: Some unicorns are white
- Because this statement implies that there is at least one unicorn that exists and is white.
 The philosophy textbook written with the student in mind!
The philosophy textbook written with the student in mind!